This unusual shape looks sort of like a coiled, corrugated garden hose – but it’s actually a mathematical shape that, until recently, were thought to be impossible to visualize in three dimensions. Flat tori were first demonstrated in the 1950s, and io9 gives a suitably adorable description of exactly how to imagine one. They say: “To imagine a flat torus, imagine a video game with a wraparound screen — for instance, if you go up the top side, you emerge from the down side. […] Imagine taking a square flat torus, wrapping it into a tube, and then bending its ends so they met to form a ring.”

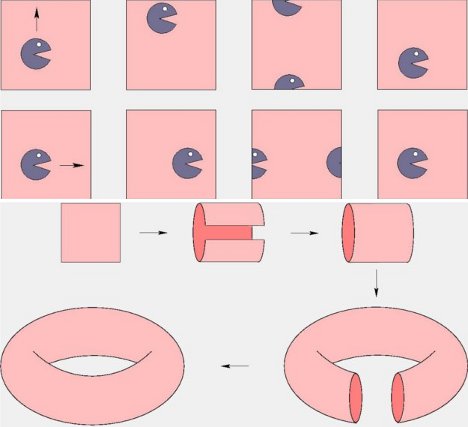
Until now, it was assumed that an object like this couldn’t be demonstrated in 3D because of the distortion that takes place with the wrapping and the bending. But researchers in France thought outside of the tube and added corrugations to the shape, overcoming the distortion problem. These surfaces are known as smooth fractals, which are somewhere between regular surfaces and fractals. Apparently the discovery could help mathematicians do their thing…but all we can think of is a sudden craving for smooth fractal donuts.